法國數學家布豐 (Comte de Buffon, 1707-1788) 在 1733 年提出了著名的投針問題：在一個平面上有距離恰好為 D 的等距直線條紋。現在我們投擲一根長度恰好為 L 的細針，請問有多少機率這根針會與直線條紋相交呢？

這個問題獲得相當大的迴響，一方面或許因為在機率論在賭博界開始默默發展的 18 世紀初，以幾何學結合機率 (Geometric Probability) 在當時是一個很新的研究領域。另一方面，布豐投針問題的答案實在是太漂亮了，而且居然跟 π 有關：當針長 L 不超過條紋間距 D 的時候，針與條紋相交的機率是 2L / (πD)，這在計算圓周率的歷史上是會絕對留名的。我們今天就用投針的方法來估計 π 之值吧。

今天除了基本的幾個函式庫以外，還需要 matplotlib 的 collections，這樣可以一口氣繪製很多線段！

from matplotlib import collections as mc

接下來就是主要的模擬丟針部分啦

# 設定間隔與針的長度
D = 1
L = 0.6

xcoords = np.linspace(0, 10 * D, 11)
for x0 in xcoords:
    plt.axvline(x = x0, color = 'k', alpha=0.7, linestyle='-')

# 設定投針的數量
N = 1000

# 模擬在一定範圍內投針
xc = np.random.uniform(0, 10 * D, N)
yc = np.random.uniform(0, 8 * D, N)
tc = np.random.uniform(-np.pi/2, np.pi/2, N)
x1 = xc - np.cos(tc) * L/2
x2 = xc + np.cos(tc) * L/2
y1 = yc - np.sin(tc) * L/2
y2 = yc + np.sin(tc) * L/2

lines = []
for i in range(N):
    lines.append([(x1[i], y1[i]), (x2[i], y2[i])])
    
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
lc = mc.LineCollection(lines, color=colors)
ax = plt.gca()
ax.add_collection(lc)
ax.autoscale()
plt.title(f"L = {L:.3f}, D = {D:.3f}")

# 計算與條紋相交的針數
count = 0
for i in range(N):
    if np.floor(x1[i]/D) != np.floor(x2[i]/D):
        count += 1

p = count / N
print(f"{N} 針當中有 {count} 根產生交點；估計的 pi 值為 {2*L/D/p:.5f}")

成果如下：

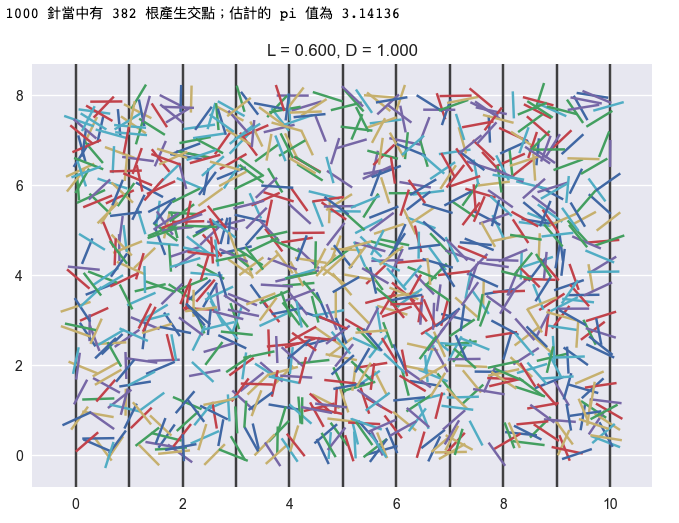
然後我在找資料的時候發現 Buffon's Needle Problem 居然有個超酷炫延伸版：Buffon's Noodle Problem XD 這個布豐麵條問題是考慮每一次丟的不是直線的針，而是一條彎曲的固定形狀。該問題是直到 19 世紀的 1860 年才被法國數學家 Barbier 提出並解決。詳情可以參考維基百科 https://en.wikipedia.org/wiki/Buffon%27s_noodle。